What is rest mass?  Brief analysis to make it clear that rest mass  has kinetic energy  

                                                  Nobuo Miyaji   in Tokyo Japan (Dated: June 20th,2012)  　   Welcome your comment
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 日本語翻訳追加　２０１２年７月９日 　　　　　

Preface  
 Many people get confused about the concept of rest mass in the theory of Special Relativity. Scientists have also deliberated
 over a rest mass.(Gary Oas1, L. B. Okun2 , Max Jammer 3). A single rest mass has been thought to be equivalent to rest energy
 because relativistic mass is divided into rest mass and kinetic energy according to Taylor expansion.

 However, there remains a question on what is rest mass. This article aims to indicate the concept of rest mass. A group of
 moving mass with arbitrary velocity also has an equivalent rest mass. A group of mass and its momentum are defined as a
 vector of Lorentz transformation. Developing this concept, there is a possibility that a single rest mass is resolved into a group
 of small rest mass , furthermore, its small rest mass is also repeatedly resolved into smaller mass. A single rest mass contains
 confined kinetic energy. In other words, inner kinetic energy is the composition of rest energy.
 
 For example, a stationary object is also composed of numerous molecules which have active molecular motion by thermal
 energy. This energy of confined motion is a part of rest mass.

 When we consider photon, we cannot see the light resting because light speed is maximum. All of the photon energy can be
 attributed to momentum not to rest energy. Rest mass of a certain object except for photon can be observed if we can
 pursue it and see it resting. In this case , we can say its macro momentum is zero because its position is not moving.
 However,we must remember inner part of rest mass has momentum in the micro world. If the total of momentum of micro
 world is zero in our stationary coordinate , observer considers it to be resting. According to this idea, it can be proved that
 rest mass has kinetic energy by mathematical analysis.
     
Modeling of a group of mass                                                                                                                           
At first, a single mass shown in Fig.1 is moving with velocity in a certain inertial coordinate A.   
Relativistic mass (wikipedia.org/wiki/Mass in special relativity4)m is well known as equation(1).
Including momentum p, m and p are expressed by matrix equation(2).

                                                                       
                                                     

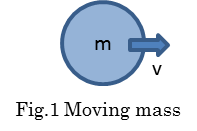
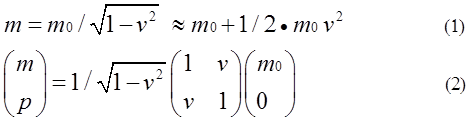
m0 is a rest mass and v is the velocity of the center of a rest mass in a coordinate A. v is defined as non-dimensional velocity divided by light speed.Equation(1),(2) are important to express that m has kinetic energy and rest energy m0. In addition, m0 is transformed into m according to Lorentz transformation. However, there remains a basic question about what is rest energy. When we observe a moving mass m at the same velocity v, m0 is stationary. Even if the center of rest mass system is resting, it should be considered that inner part of rest mass is not resting.

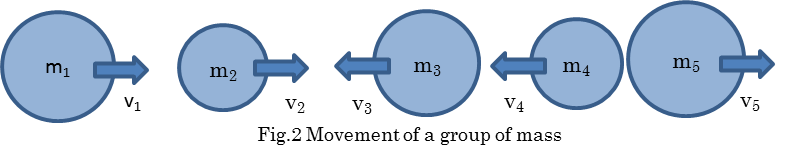
 To make it clear what is rest mass, it is possible to suppose that a lot of mass are moving in a coordinate A as shown in Fig.2. Among a group, mi is a mass and vi is the velocity of mass in the preceding coordinate A.

                       
Generalized application of Lorentz transformation.

Mass and momentum are expressed by follwing expression in the coordinate A
                                                             
                                                                             

A group of mass is observed from a different coordinate B. Coordinate B is moving with velocity V in the coordinate A. There is always a coordinate where a group of mass is considered to be stationary. According to the formula of synthesis of velocity, vi is converted into vi’ in the coordinate B. Velocity vi’ is expressed by equation (5). Using equation (5), mi’ and pi’ are expressed by equation (6),(7).

                                                                                            

Equation (8) is always true.

                   　　      

By substituting equation (3),(4),(8) into equation (6), (7), equation (9), (10) are obtained.

                         

                                　　  
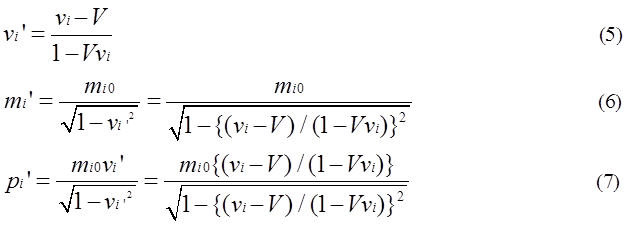
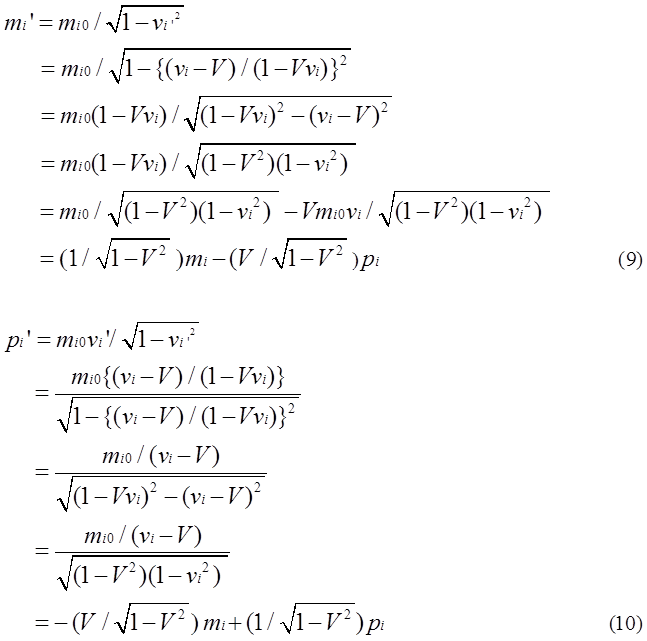
The sum of mi and pi are expressed by following equations.

                    　　     

                    　　     

A group of mass and momentum are defined as following.These equations mean that mass M(total energy) is the
summation of relativistic mass mi and P(total of momentum) is summation of momentum pi.M' and P' have the same
meaning respectively.  

　　　　　　　　　　                                                        

Equations (11), (12) are expressed by a matrix equation.

               　　 　              

          

Equation (14) is exactly Lorentz transformation of a group of mass and momentum similar to the fundamental equation (2).
This equation implies that a group of mass has an invariant as a rest mass as well as a single mass. A group of mass becomes a rest mass when its momentum P' is zero in coordinate B.
When we choose a coordinate B which makes P’ equal zero, P=MV is obtained from the second line equation of matrix equation (14). Using the relation of P=MV, the first line equation of matrix equation (14) is following.

            　  　          


Referring to the relation P=MV, equation (16) is obtained. M’ can be considered as an equivalent rest mass M0. M0 is the
summation of relativistic mass mi’.　In this case, relativistic mass is important to define the rest mass of a group of mass.

　　 　　　　　　　　　　
From equation (6) and equation(13), equivalent rest mass M’ is larger than the total of rest mass mi0.Despite the fact
that mi' is moving, M' is considered to be staionary in coordinate B which makes P’ equal zero.
                  　    　                         

Equation(18) indicates a sigle mass m has an invariant. Equation(19) also means a group of mass M has an invarinat.
Only when a group of rest mass is confined within M0, M has an invariant in any reference system.
                       
 
 
In considering a rest mass, it is not a mathematical point but a compound of smaller particles which contain kinetic energy and rest energy. And then, resolved rest energy of smaller particles has also kinetic energy and rest energy.

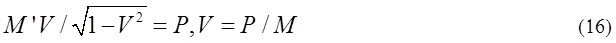
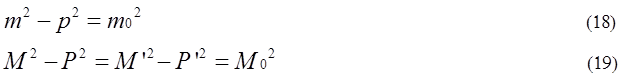
    Conclusion


Mathematical analysis concerning a group of rest mass and momentum helps to understand the concept of rest mass.


1) A group of mass and a group of momentum can be defined as a vector of Lorentz transformation. Furthermore, the velocity of a group of mass can be decided, and the moment of a group of mass is converted to zero in the moving coordinate with the velocity. 
    
2) Equivalent rest mass M0 is larger than the total of inner rest mass. That means confined kinetic energy is the composition of rest energy.
    
3) There is a possibility that a single rest mass can be infinitively resolved into a group of small mass by repeating procedures of resolution.

   <Postscript>

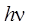 We can imagine an extreme case. The smallest rest mass may be composed of two photons with symmetrical momentum
 in a certain coordinate. The origin of rest mass may be photon energy which is attributed to electromagnetic field energy.

<reference>

1 Gary Oas, On the abuse and use of relativistic mass, physics.ed-ph 21 Oct 2005 p1-2

2 LL. B. Okun (1989), "The Concept of Mass", Physics Today 42 (6): p31–36

3 Max Jammer (1997), Concepts of Mass in Classical and Modern Physics, Courier Dover Publications, p179, ISBN 0486299988

4 http://en.wikipedia.org/wiki/Mass_in_special_relativity

Visit URL  http://miyajiphysics.info

Translation of the article into Japanese.

　　　静止質量とは何か？　　　　簡潔な解析による質量集団が静止質量と運動エネルギを持つことの証明

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　宮地宣夫による　翻訳　２０１２年７月９日

　　序言

多くの人々は特殊相対論の静止質量の概念について混乱している。科学者達も静止質量について考察してきた。
(Gary Oas1, L. B. Okun2 , Max Jammer 3)一個の静止質量は静止エネルギと等価であると考えられてきた。というのは相対論的
質量の式をテーラー展開すると静止質量と運動エネルギに分離できるからである。

しかし、式の展開後も、静止質量とは何かの問題は残る。この記事は静止質量の概念を示すことが目的である。各々の質点が
任意の速度で動く質量集団もまた等価的な静止質量をもっている。質量集団の質量と運動量はローレンツ変換のベクトル
として定義できる。（ここでは時間軸とX軸のみ）この考え方を発展させて、一個の静止質量はより小さい静止質量に分解できる。
（見かけは静止していても、止まっている質量でなく運動する質量に分解できる。)
更に、その小さい静止質量も繰り返してより小さい質量に分解できる。一個の静止質量は閉じ込められた運動エネルギを含む。
つまり、内部の閉じ込められた運動エネルギは静止エネルギの成分である。

例として、止まっている物体は、熱によって分子運動する無数の分子で構成されている。この閉じ込められた運動エネルギは静止
エネルギの一部である。

光子を考えると、光子を止まって見ることはできない。光速は最大速度であるからだ。光子エネルギはすべて運動量であって静止
エネルギではない。光子以外の物体は、それを追跡して、静止しているのを見ることができる。この場合、物体の位置が動かないの
で、巨視的な運動量はゼロであると言える。しかし、静止質量は内部の微視的世界で運動量を持つことを覚えておく必要がある。
内部の運動量の合計がゼロならば、観測者の静止系でその物体が静止していると見なされるのである。この考えに従えば、言葉
でなく、数学的解析を使って静止質量は運動エネルギをもつことが証明される。

　　質量集団のモデル化


最初に、ある慣性座標系Aで図１に示す単一の質量が速度Vで動くことを想定する。相対論的質量は有名な式（１）で示される。
(wikipedia.org/wiki/Mass in special relativity4)

運動量ｐを含めると、質量ｍと運動量ｐはローレンツ変換の行列の式（２）で示される。　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　

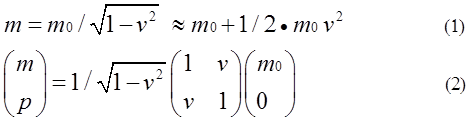
ｍ０は静止質量、ｖは静止質量の中心（運動量ｐの中心）の速度である。ここでの速度は光速で割った無次元速度である。
式（１）、（２）は重要で、ｍは運動エネルギと静止エネルギｍ０を持っていることを示す。さらに、（ｍ０、0）はローレンツ変換により
（ｍ、ｐ）に変換される。（ｖの速度をもつ移動座標系ではｍ＝ｍ０、ｐ＝0）
しかし、一個の質量のみ考えていると、静止質量とは何かという基本的問題は残されている。一個の質量を同じ速度ｖで観察する
と、ｍ０は静止している。たとえ静止質量中心が止まっていても、質量の内部は静止していないとすべきである。

静止質量とは何かを明らかにするために、図２に示されるように、多数の運動する質量を想定することができる。
図２の集団の中で、ｍｉは質量で、ｖｉは前述した座標系Ａにおける速度である。


　　　　　　　　　　　　　

　　ローレンツ変換の一般化された応用

個々の質量と運動量は座標系Ａで以下の式で示される。これは、式（１）、（２）と同様である。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　

質量集団は違った座標系Ｂでも観測できる。座標系Ｂは慣性系Ａに対して一定速度Ｖで移動する座標系とする。いつも必ず質量
集団が静止していると見なすことができる特別な座標系が存在する。式（３）、（４）を特殊相対論の速度合成の公式に従ってｖｉを
座標系Ｂの速度ｖｉ’に変換すると式（５）となる。式（５）を使って、座標系Ｂにおける質量ｍｉ’と運動量ｐｉ’は式（６）、（７）で示される。


　　　　　　　　　　　　　　　　
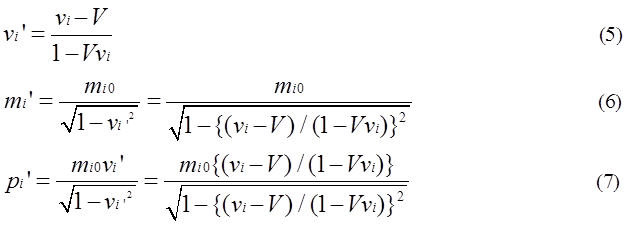
式（８）は常に成り立つ。（以外かもしれないが検算すれば確かでである。）

　　　　　　　　　　　　　　　　

式（３）、（４）、（８）を式（６）、（７）に代入すると式（９）、（１０）が得られる。

　　　　　　　　　　　　  　　　　　

　　　　　　　　　　　　
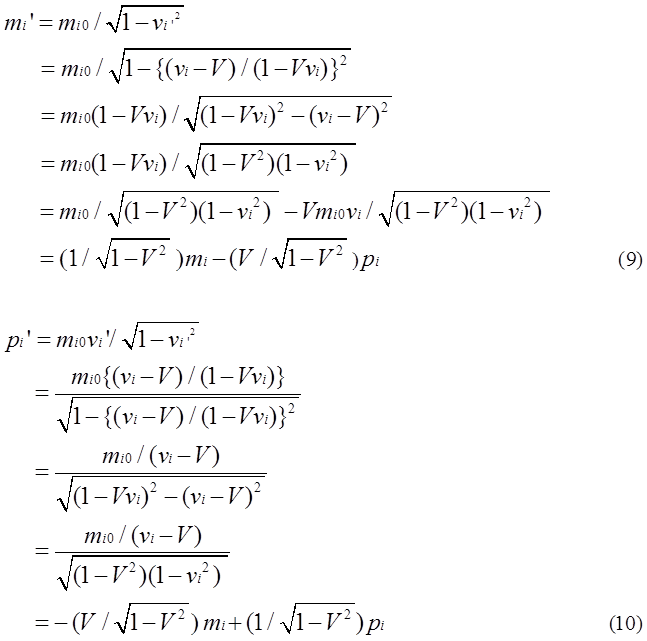
ｍｉとｐｉについて総和をとると式（１１）、（１２）が得られる。

　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　

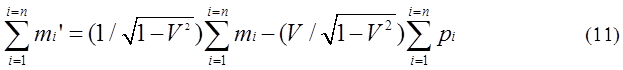
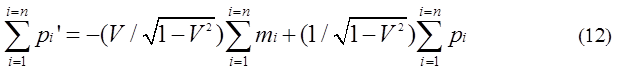
集団の質量Ｍと運動量Ｐは次のように定義できる。これら式は質量Ｍ（全エネルギ）は相対論的質量の和であり、Ｐ（運動量）は
運動量ｐｉの総和であることを意味する。Ｍ’　とＰ’の式も同様の意味を持っている。   

             　                                                             

式（１１）、（１２）は行列の式で表される

                 　             

式（１４）はまさしくローレンツ変換の式で式（２）と同様である。
この式は動く質量集団は静止質量としての不変量をもつことを意味する。一個の運動する質量と同様である。座標系Ｂで集団の
運動量ｐｉ’の和であるＰ’がゼロならば、Ｍ’は静止質量になる。ちょうどＰ’がゼロとなるような座標系Ｂを選択すれば、式（１４）の行列
の２行目式からＰ＝ＭＶが得られる。 Ｐ＝ＭＶの関係式を使って、行列の１行目の式から式（１５）が得られる。

　　　　　　　　　　　　　　　


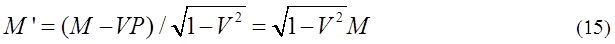
Ｐ＝ＭＶの式を参照すれば、Ｍ’は等価的な静止質量Ｍ０とみなせる。Ｍ０は相対論的質量ｍｉ'の総和である。この場合、
相対論的質量は質量集団の静止質量を定義する上で重要である。

　　　　　　　　　　　　　　　

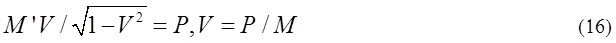
式（６）、（１３）から等価的静止質量Ｍ’は、ｍｉ０の合計値よりも大きい。各々のｍｉが速度ｖｉで動くと仮定した事実にかかわらず、
特別な座標系Ｂでは運動量の総和はＰ’＝０となるので、Ｍ’は静止している質量とみなされる。

                   　　                              


式（１８）は一個の質量は不変量を持つことを示す有名な式である。式（１９）もまた集団の質量Ｍは不変量を持つことを示す。
集団が（外力によってばらばらにならないで）、Ｍ０内に閉じ込められている限り、Ｍはどんな慣性系についても不変量Ｍ０を持つ。
            　　　　   　  

 
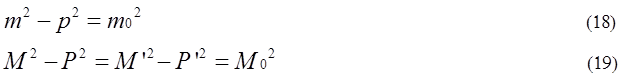
静止質量を考慮するとき、それは数学的点ではなく、より小さい粒子の合成物である。構成粒子は運動エネルギと静止エネルギ
を含んでいる。それで、さらに繰り返し分解されたより小さい粒子のエネルギも同じく運動エネルギと静止エネルギを持っている。

　　結論


質量集団の静止質量と運動量の数学的解析は静止質量の概念を理解する上で役立つ。

１）質量と運動量の集団はローレンツ変換のベクトルとして定義できる。さらに、集団の速度は計算でき、集団の代表速度で動く
　　座標系ではゼロになる。

２）等価的静止質量Ｍ０は内部静止質量よりも大きい。それは、運動エネルギが静止質量Ｍ０の成分であることを意味する。

３）一個の静止質量は繰り返し分解操作を実行すれば、小さい質量へと無限に分解される可能性がある。


　　後書
　
極端な場合を想定することが出来る。最小の静止質量は、ある座標系で２個の対称な運動量をもつ光子で構成されている可能
性がある。静止質量の起源は電磁場の光子のエネルギかもしれない。

 　<参考引用資料>

1 Gary Oas, On the abuse and use of relativistic mass, physics.ed-ph 21 Oct 2005 p1-2

2 LL. B. Okun (1989), "The Concept of Mass", Physics Today 42 (6): p31–36

3 Max Jammer (1997), Concepts of Mass in Classical and Modern Physics, Courier Dover Publications, p179, ISBN 0486299988

4 http://en.wikipedia.org/wiki/Mass_in_special_relativity

　＊海外向けのより進んだ内容を掲載した記事　  http://miyajiphysics.info